”Varmaan suurin kynnys aloittamiseen ovat ihan puhtaan konkreettiset asiat. Siispä kysyisin, että olenko ymmärtänyt asiat oikein ja lisäksi muutaman lisäkysymyksen.”

Maunun koulun opettaja Marko Mäenpää innosti minua vastamaan julkisesti hänen konkretiaa ja selkeyttä vaativiin kysymyksiin. Tässä siis Markon kysymyksiä ja minun vastauksiani niihin:

Näinkö minun pitäisi toimia käytännössä?

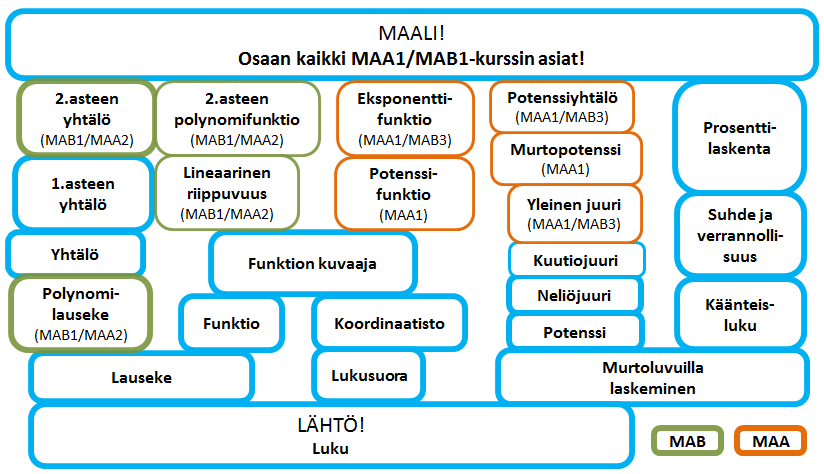
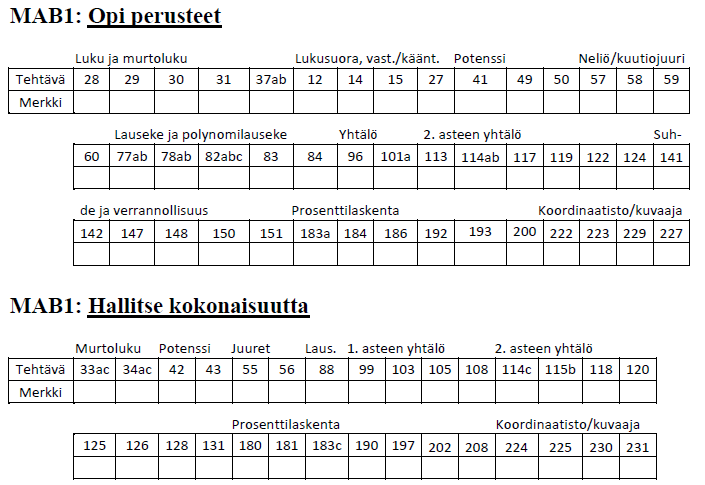
”Step 1) Jaan esim. 7 luokan oppisisällöt noin 2 viikon kokonaisuuksiin ja teen käsitekartat ja vihkoon liimattavaan seurantataulukkoon mietimme kuhunkin kokonaisuuteen sopivat tehtävät perusteiden hallintaan ja kokonaisuuksien hallintaan.”

Kommentti: Kyllä, näin homma lähtee käyntiin. Se kannattaa kuitenkin huomioida, että opettajan järkeilemä ”2 viikon kokonaisuus” saattaa nopeimmalle oppijalle olla vain viikon urakka ja hitaammalle oppijalle se voi olla kolmen viikon urakka. Jotta kenenkään oppimista ei jarruteta (ja oppimisen intoa ja motivaatiota tuhota) ja jotta ketään ei pudoteta kyydistä, tämä eritahtinen oppiminen kannattaa ehdottomasti mahdollistaa sopivin opetusjärjestelyin.

”Step 2) Kerron oppilaille miten uusi systeemi menee ja käymme yhdessä läpi kartat ja taulukot, niin jaan heidät pienryhmiin osaamistason mukaan. Liimataan monisteet vihkoihin ja jaetaan värikynät.”

Kommentti: Pienryhmät ovat erittäin hyvä juttu oppimisen kannalta, mutta itse en jaa niitä osaamistason mukaan. Se voisi olla hyvä juttu, mutta olen antanut oppilaiden vapaasti valita oma ryhmänsä. Heterogeenisissä kaveriporukoista koostuvissa pienryhmissä on se etu, että nopeammat oppijat oma-aloitteisesti neuvovat ja opettavat kavereitaan, jolloin sekä ”opettajan”  että opetettavan osaaminen lisääntyy. Lisäksi siinä opitaan vuorovaikutustaitoja ja sosiaalisia taitoja. Homogeenisissä ryhmissäkin on varmasti omat etunsa, mutta kumpi on parempi, se selviää kokeilemalla.

”Step 3) Hypätään veteen. Ts. aloitetaan laskeminen. Meillä on käytössä tabletteja ja jonkin verran videoita mutta teorian voinee lukaista myös oppikirjasta tai ensimmäisen tunnin teorian voin minäkin pitää. Sitten aloitetaan laskemaan ja teoriaa voi kerrata tarvittaessa kirjasta tai jos on video ko. aiheesta. Opettaja kiertää auttamassa ryhmiä pois jumeista.”

Kommentti: Juuri näin. Kokemukseni mukaan kirja on se, josta kaikkein hanakammin opiskellaan teoriaa. Moni opettaja on ällistellyt, miten tämä menetelmä lisää radikaalisti oppikirjojen lukemista (lue esimerkiksi täältä).

”Step 4) Pidetään kokeita sitä mukaa, kun oppilaat saavat perusasiat opittua.”

Kommentti: Tämä on mielestäni oleellinen asia, mikä kannattaa mahdollistaa. Viereisessä yläkoulussa opettajat ovat toimineet näin ja se on ollut hyvä systeemi. Oppilaat, jotka eivät ole osanneet kaikkia juttuja, on ohjattu harjoittelemaan niitä lisää. Tällöin ehkäistään tiedollisten puutteiden syntymistä ja kasaantumista (lue: mastery learning) He, jotka osaavat välitestin kaikki asiat, saavat jatkaa eteenpäin siitä missä sillä hetkellä ovat. Me emme ole tätä osanneet lukiossamme vielä koeviikkojen ja oman ahdasmielisyytemme takia mahdollistaa, mutta siihen tulee muutos ensi vuonna. Aiomme alkaa opettaa oppimisen ehdoilla, emme kalenterin ehdoilla. Tarkemmat toimintamallit ovat vielä suunnittelupöydällä, niistä lisää tässä blogissa ensi vuonna.

Tarkentavia kysymyksiä

1) Mitä eroa on käsitekartalla ja oppimispolulla tässä tapauksessa?

Vastaus: Itse ajattelen noita oikestaan samoina asioina. Olen tällä hetkellä sitä mieltä, että oppimispolku (tai käsitepolku) on ehkä parempi ja toimivampi nimitys ja malli.

2) Miten oppilas tietää koska hän värittää asian käsitekartalta?

Vastaus: Silloin, kun hän kokee ymmärtävänsä ja osaavansa asian. Tämä on alussa oppilaille erittäin vaikeaa, varsinkin jos he ovat tottuneet, että opettaja aina arvioi heidän osaamisensa heidän puolestaan. Heillä voi olla heikko itsetuntemus tai minäkäsitys, he voivat olla arkoja arvioimaan omaa osaamistaan. Jos oppimisympäristö on turvallinen, ahdistusvapaa (lue: luodaan ahdistusvapaa koulu) ja kannustava, tällä menetelmällä he vähitellen voivat oppia arvioimaan omaa osaamistaan realistisesti ja heidän itsetuntonsa ja minäkuvansa on mahdollista kehittyä vahvemmaksi.

3) Miten käsitekartta ja tehtävätaulukko liittyvät toisiinsa?

Vastaus: Itse pohdiskelen sitä, että käsitekartan ja tehtävätaulukon seuraava kehitysversio voisi olla niiden yhdistelmä. Eli tehtävänumerot voisi ehkä sijoittaa suoraan käsitekartan laatikoihin. Tosin se ei ole ongelmaton, koska vaikka joku tekee kaikki yhden käsitteen tehtävät, ei hän välttämättä vielä täysin ymmärrä sitä. Pitäisikö laatikkoon olla mahdollista lisätä tehtäviä? Jos keksit tähän jonkin hyvän ratkaisun, kuulisin sen mielelläni!

4) Missä välissä oppilaiden tehtäviä käydään läpi?

Vastaus: Oppilaat käyvät tehtäviä läpi pienryhmissä keskustelemalla niistä samalla kun he ratkovat niitä. Tai kun he neuvovat toisiaan. Jos koko ryhmä ei osaa jotain tehtävää, tai he ovat tehneet sen väärin, voi opettaja keskustella tehtävästä pienryhmän kanssa ja samalla se tulee käytyä läpi. Koko luokan yhteiset tehtävien läpikäyntisessiot ovat usealle oppilaalle turhia ja täyttä ajan hukkaa (he osaavat tehtävät jo, tai heillä ei ole vielä riittävästi tietotaitoa, jotta he voisivat ymmärtää läpikäytävät tehtävät siinä ajassa, jossa ne käydään läpi). Tämä on hyvä keino tappaa motivaatiota ja tukahduttaa orastavaa innostusta. Opettajat: lopettakaa tämä!

5) Kuka kommentoi oppilaiden tehtävät vihkoon ”oikein” tai ”väärin” ja ympyröi laskuvirheet?

Vastaus: Useimmiten oppilaat itse. Jos oppilas ei itse löydä laskuvirhettä, niin samalla kun kierrän neuvomassa oppilaita ympäri luokkaa, saatan ohimennen lukaista virheellisen ratkaisun ja ympyröidä itse virheen. Tämän jälkeen oppilas alkaa korjaamaan ratkaisuaan ja minä siirryn auttamaan seuraavaa oppilasta/pienryhmää.

6) Meillä on nyt kolme jaksoa ja siis keskimäärin 6 koetta lukuvuodessa. Onko ajatus vain kylmän rauhallisesti odottaa, että viimeinenkin on saanut perustason läpi ja sitten aiheesta pidetään yhteinen koe? Mites ne kevään viimeiset kurssit?

Vastaus: Kyllä, ja tässä testataan opettajan hermoja, malttaako hän odottaa riittävän pitkään, vai pudottaako hän hitaammat kyydistä. Itse harkitsen nyt, että tekisin näitä ”2 viikon kokonaisuuksia” ja tekisin jokaisesta kokonaisuudesta sähköisen testin, jonka voi tehdä milloin haluaa. Jos testin läpäisee (osaa kaiken tai lähes kaiken), voi siirtyä eteenpäin, jos ei läpäise, kertaa vielä sitä aihetta, jonka jälkeen tekee testin (tai eri testin samasta aiheesta) uudestaan. Ja taas jos ei läpäise, niin ei muuta kuin lisää harjoittelua. Tällöin kenenkään oppimista ei jarruteta ja kukaan ei myöskään hypi liian nopeasti aiheesta toiseen, jolloin tiedollisia aukkoja ei pääse syntymään ja jokainen saa vähintäänkin vahvat perustiedot ja taidot (lue taas: mastery learning). Tätä systeemiä minulla ei siis vielä ole käynnissä, mutta yritän saada sen toimintaan tammikuusta alkaen. Jos saat tämän toimimaan ennen minua, kerro miten sujuu!

7) Kotitehtävät?

Vastaus: Kenellekään ei tarvitse antaa tiettyjä kotitehtäviä. Voit esimerkiksi kannustaa oppilaita tekemään n kappaletta kotitehtäviä oppituntien jälkeen siitä aiheesta, missä sillä hetkellä ovat. He saavat siis itse valita omat kotitehtävät oman sen hetkisen motivaation, tavoitteen ja aikataulun mukaan. Kokemuksesta voin sanoa, että jotkut eivät välttämättä tee mitään kotona, jotkut taas ahkeroivat hulluna (kerran yksi oppilas teki yli 60 lukion matematiikan tehtävää yhden viikonlopun aikana). Autonomia on todistetusti yksi motivaatiota lisäävä tekijä.

8) Mihin asioihin kiinnität arvioinnissa huomiota? Mitä keräät?

Vastaus: Itse olen tähän mennessä teettänyt kurssikokeen, mutta en enää pidä siitä menetelmästä yhtään. Läheisen yläkoulun opettajat ovat päässeet jo tilanteeseen, missä kokeet ovat heille merkityksettömiä. Ei niitä tarvitse enää teettää. Itse pohdin, että jos otan käyttöön ne ”2 viikon kokonaisuudet”, niin jos nämä kaikki läpäisee, niin silloinhan arvosanan pitäisi olla vähintään 7-8. Ehkä noiden päälle voisi oppilaiden itsearvioinnin avulla ja oppituntien aikana käytyjen oppilas-opettaja-keskusteluiden perusteella päätellä, että kuka saa kasin, kuka ysin ja kuka kympin. Erillistä kurssikoetta aion kyllä vältellä, jos vain mahdollista.

Eikö olisi mahtavaa, jos huonoin arvosana jonka antaisi, olisi 7! Mutta toisaalta kuten kysyit, ”entäs ne kevään viimeiset kurssit?”. Tämä kysymyshän koskee vain hitaimpia oppijoita ja tässä tuleekin kysymys, pitäisikö kaikki asiat yrittää oppia hätäisesti kiireellä, jolloin todellinen oppiminen lähentelee nollaa ja ahdistus ja matematiikka-inho on taattu, vai pitäisikö rakentaa vahvaa perustaa, vaikka oppisikin vähemmän kuin muut?

Kiitos Markolle loistavista kysymyksistä! Lisäkysymyksiä voi lähettää yksityisesti osoitteeseen pekka.peura (at) maot.fi, tai sitten suoraan alla olevaan kommenttipalstaan.