Martinlaakson lukiossa tehtiin elo-syyskuussa 2012 kokeilu, jossa lukion MAA1- ja MAB1-kurssin opiskelijoita opetettiin samaan aikaan samassa tilassa. Järjestely osoittautui toimivammaksi kuin perinteinen jako MAA1- ja MAB1-ryhmiin, ja se myös kannusti aiempaa useampaa opiskelijaa jatkamaan pitkän matematiikan opintoja. Ensimmäisen kurssin jälkeen MAA2-kurssille jatkoi 112 opiskelijaa ja MAB2-kurssille 32 opiskelijaa! (Martinlaakson lukio on yleislukio, jonka painopistealueet ovat draama ja teatteri sekä LUMA-aineet. Lukion sisäänpääsykeskiarvoraja v.2012 oli 7,92.)
Elokuussa lukiomme 144 ensimmäisen vuosikurssin opiskelijaa jaettiin viiteen ohjausryhmään (12A, 12B, 12C, 12D ja 12E). Ensimmäisessä jaksossa opiskelijat pysyivät kaikilla kursseilla omina ryhminään. Järjestelyn tarkoituksena oli helpottaa opiskelijoiden ryhmäytymistä uudessa koulussa. Aikaisempina vuosina opiskelijat oli matematiikan oppitunneilla jaettu ohjausryhmiä sekoittaen erikseen pitkän ja lyhyen lukijoihin, mutta tänä lukuvuonna opiskelijat olivat myös matematiikan tunneilla yhdessä oman ohjausryhmänsä kanssa.
Yksilöllisen oppimisen opetusmenetelmä tekee kursseista joustavia
Yksilöllisen oppimisen opetusmenetelmä (lue lisää: perusajatus, kokemuksia ja mastery learning) mahdollistaa käytännössä sen, että yksi opettaja voi samassa tilassa samaan aikaan opettaa oppimisprosessin eri vaiheessa olevia opiskelijoita. Sillä ei ole merkitystä, millä kurssilla tai tasolla opiskelijat ovat.
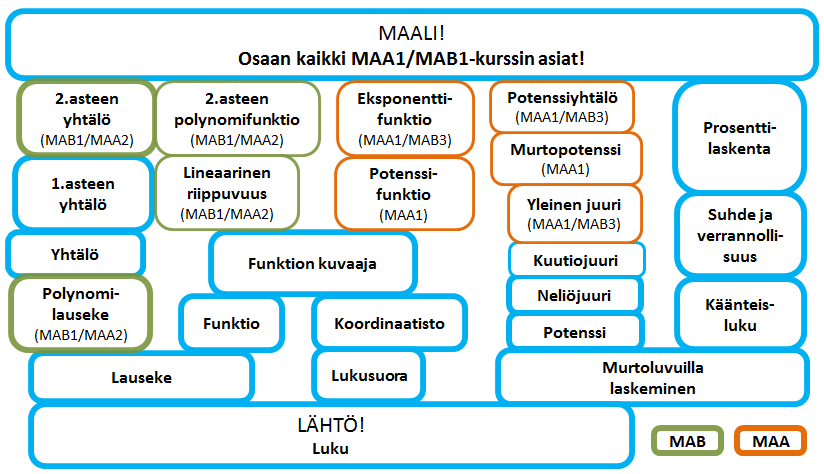
Ensimmäisellä oppitunnilla opiskelijoille kerrottiin käytännön järjestelyistä ja heidät perehdytettiin analysoivaan tapaan ratkaista harjoitustehtäviä, jolloin harjoitustehtävien avulla jokaisen yksilölliset virhekäsitykset saadaan sekä opettajan että opiskelijan omaan tietoisuuteen. Näin opetusta pystytään kohdentamaan henkilökohtaisella tasolla ja oppiminen on tehokkaampaa. Opiskelijat liimasivat myös vihkoihinsa MAA1- ja MAB1-kurssien ”käsitehaitarin” ja heitä neuvottiin värittämään käsitelaatikko aina, kun he kokivat ymmärtävänsä kyseisen käsitteen.
Käsitehaitarissa on visuaalisesti nähtävissä kurssin sisältö, ja siihen on pyritty hahmottelemaan käsitetorneiksi sitä, miten käsitteet liittyvät toisiinsa. Se auttaa myös opettajaa ja opiskelijoita visuaalisesti havaitsemaan, miten paljon yhteistä MAA1- ja MAB1-kursseilla on ja miltä osin kurssit sisällöllisesti poikkeavat toisistaan.
Kurssilla käytettiin kahta oppikirjaa
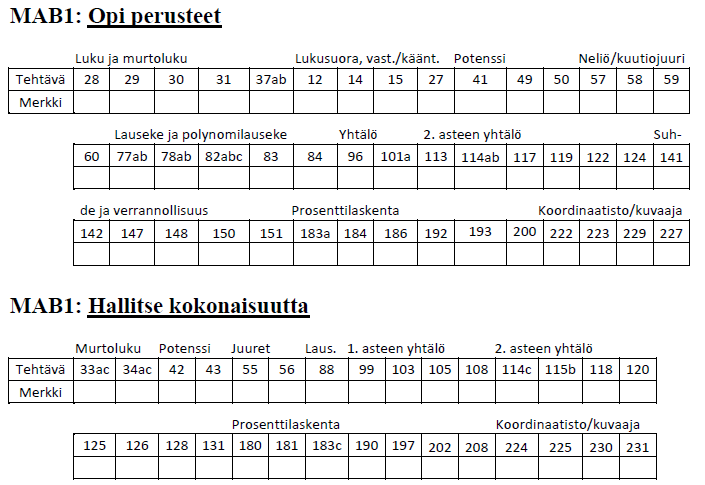
Opiskelijat saivat itse valita, kummalla tasolla he matematiikkaa halusivat opiskella, ja valintansa perusteella he hankkivat kyseisen tason oppikirjan. Opiskelijat saivat ensimmäisellä tunnilla käsitehaitarin lisäksi myös joko MAA1- tai MAB1-tehtävälapun, jossa olivat nähtävillä koko kurssin harjoitustehtävät ja johon he merkitsivät, osasivatko he tehtävän vai oliko heillä virhekäsityksiä kyseisen tehtävän ratkaisemisessa.
Tehtävälapun ja omatahtisen oppimisen hyödyt
Vihkoon liimattu tehtävälappu ja omatahtinen opiskeluvauhti olivat hyödyllinen yhdistelmä monella eri tapaa. Tehtävälappu ohjasi opiskelijoita etenemään kurssilla tietyssä järjestyksessä käsitteeltä toiselle ja omatahtisuus mahdollisti sen, että ketää ei pakotettu etenemään opinnoissa seuraavaan käsitteeseen, ennen kuin edellinen oli sisäistetty (vrt. mastery learning). Vastaavasti kenenkään ei tarvinnut odotella muita, jos jotkin asiat olivat jo entuudestaan tuttuja tai nopeasti omaksuttavissa, ja näin jokainen pystyi edetä opinnoissaan juuri omaa henkilökohtaista oppimistaan tukevaa vauhtia. Tehtävälappu ja omatahtisuus estivät myös ”putoamisen kyydistä”, koska jos joku oli esimerkiksi muutaman päivän sairaana, niin tullessaan takaisin kouluun hänen opintonsa kurssilla oli juuri siinä kohdassa, mihin hän oli edellisellä kerralla jäänyt. Tai vastaavasti hänen on ollut mahdollista myös jatkaa opintoja kotonaan, koska tehtävälapusta näkee aina seuraavan harjoiteltavan tehtävän/käsitteen. Muun muassa nämä seikat tekevät oppimisesta mielekkäämpää ja opiskelumotivaatio pysyy hyvällä tasolla.
Yksilöllisen oppimisen opetusmenetelmä ja yllä kuvatut yksinkertaiset ”apuvälineet” tekevät myös opettajan työstä mielekkäämpää, koska enää opettajan ei tarvitse kiireessä ja tiukassa aikataulupaineessa vetää suuria massoja kivireen tavoin eteenpäin kurssilla, vaan opettajan on mahdollista kohdata jokanen oppija yksilöinä ja räätälöidä opetusta kullekin oppijalle sopivalle tasolle. Lisäksi opettajan kokonaistyötaakka vähenee, koska oppituntien välissä ei tarvitse suunnitella seuraavan oppitunnin esitystä. Riittää, että menee oppitunnille ja auttaa jokaista oppijaa siinä aiheessa ja sillä tasolla, joka tukee hänen oppimistaan sillä hetkellä parhaalla mahdollisella tavalla. Opettaja pääsee tosissaan käyttämään omaa pedagogin ammattitaitoaan!
Järjestelyn hyödyt aiempaan käytäntöön verrattuna
Järjestelyn yhtenä pääajatuksena oli helpottaa opiskelijoiden oman tason löytämistä ja siirtymistä tasolta toiselle. Nyt käytännössä kävikin siten, että muutama ujo ja omiin kykyihin epäluuloisesti suhtautunut opiskelija oli aloittanut opintonsa lyhyellä matematiikalla, mutta muutaman viikon jälkeen, kun he olivat havainneet omat kykynsä riittäviksi ja jo omaksuneet kaikki MAB1-kurssin sisällöt, heille pystyttiin luontevasti tarjoamaan opastusta puuttuvien MAA1-kurssin sisältöjen oppimisessa. Kurssikokeena he sitten tekivät MAA1-kurssin kokeen. Ei ollut siis mitään väliä, aloittiko opiskelija lukiouransa lyhyen vai pitkän matematiikan kurssilla, vaan kaikki alkoivat opiskella matematiikkaa, ja vasta ensimmäisen jakson lopussa jokaisen piti vasta tehdä valinta, suorittaako MAA1- vai MAB1-kokeen.
Siirtyminen tasolta toiselle ei siis vaatinut siirtymistä luokkatilasta toiseen, ei vaihtamaan opettajaa eikä vaihtamaan opiskelutovereita. Riitti, että liimasi toisen tehtävälapun vihkoon ja avasi toisen oppikirjan. Opettajaa tässä järjestelyssä ilahdutti myös se havainto, että opiskelijat pystyivät luontevasti omissa pienryhmissään opiskelemaan vieretysten sekä pitkää että lyhyttä matematiikkaa ja se tuntui sekä opettajasta että opiskelijoista ihan luonnolliselta tavalta toimia. Matematiikka on kuitenkin pohjimmiltaan universaali kieli. Sitä ei ole pakko lokeroida, jotta sitä voisi oppia.